- in General by Cesar Alvarez
In-Sample and Out-Of-Sample Testing
I am frequently asked if I do out-of-sample testing. The short answer is not always and when I do, it is not how most people do the test. There are lots of considerations and pitfalls to avoid when doing out-of-sample testing. Out-of-sample testing is not the panacea it is made out to be. There are lots of grey areas which I will discuss below.
Definition
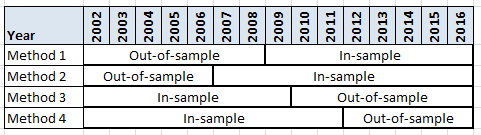
To do in-sample (IS) and out-of-sample (OOS) testing, one first divides their historical data into two parts. The most common methods for dividing the data are 50% IS/50% OOS and 67% IS/33% OOS. I will be using 15 years of data. Here are some ways that one can divide the data.
There are different reasons one may want the IS data to be the oldest data or the newest data which I will discuss below.
The IS data is used to create and optimize your strategy. After refining your strategy, you choose one variation to test on the OOS sample data. From the OOS result, one must decide if the result is good enough to say that the strategy continued to work and was not overfit to the IS data. If it passes your criteria, one can then start trading the strategy. If it does not, well it is game over on that strategy.
When I don’t use OOS testing
The most common reason not to use OOS testing is because of lack of data. I trade a VXX/XIV strategy I can only test back to 2011. There are just not enough trades to justify breaking the data into two. How do I know that strategy is not overfit? I don’t. I often will use parameter sensitivity testing as described in this post. Here my real trading becomes the OOS test, which is the best OOS test one can have.
Out-of-sample Issues
Past is likely very different from today
Even though I have data back to the 1990’s, I don’t like going that far back for my data because those markets differ greatly from we have today. This is the time before decimalization, high-frequency trading, government invention, lots of ETFs and many more changes. I will go with 15 years of data.
What is the size and period of OOS?
The first big decision to make is what period to use as the IS period and what period to use for the OSS along with how big each will be. I use the most recent data as my IS period and the older data for the OOS period. The reason for this is I want to optimize my strategy on the most recent market because I believe that is more likely to be closer to the future market than the farther out period. I want to capture a full market cycle of bull and bear when doing this. As to size I typically go with the 67/33 method. In the next post, I will show how the decision of which period to OSS can lead to very different results.
Only taking one bite of the apple
One of the core tenets of OOS testing is taking only one bite of the apple. Meaning you only test once on the OOS data to see if your strategy holds up. This is hard to do because it is against human nature. You spend weeks or months developing a strategy, and then a quick test on OOS testing fails. No one wants to throw away all that work.
But here is the more subtle thing. What is a second bite? Meaning I tested a mean reversion strategy and it failed in OOS. Does that mean I can test no more mean reversion strategies? Of course not, that would be crazy. How much does one need to change a current strategy to make it different enough to use that OOS data? Is changing parameter values to something one did not test enough? Not in my book. What about adding a new rule, say a moving average cross? Still probably not enough? What if I remove a rule and add profit target? Maybe.
There is no clear change to strategy when it is OK to use the data again. It is up to each individual to decide and that means we are likely to fool ourselves and say that small change is enough.
Also we have knowledge about our test period. I know from experience that mean reversion trading diid well from 2003 to 2009. If I use 2002 to 2006 as my OOS sample data for a mean reversion test, is that cheating?
Defining success
The above issues are not even that big to me. These next two are huge ones for me.
When we run our strategy on the OOS data, how do we know that it passed the OOS test? First, the strategy will probably not perform as well because it was developed on the current market conditions and now it is being tested on different ones. Just because it made money doesn’t make it pass the OOS test. What if the CAGR only dropped a little? That sounds like a pass. But what if that is the worst CAGR if you ran all your original 1000 variations on the OOS data? Now it doesn’t sound good.
How about a goal of beating a simple strategy? Buy the SPY when it crosses above its 200 day moving average and sell when it closes below it. Can we beat that CAGR by more than 100%? I use this idea and another which I will explain in the next post.
Picking only one variation
Now this is where I have my biggest issue with how OOS testing is normally done. For example, we have a strategy with 1,000 variations. We go through some method to pick one to test on the OOS data. See this post on how I would pick The One. Now we run The One on the OOS data and make our decision. Say our strategy did “poorly,” that means we should stop and consider this a failure.
Here is where I have my problem. What if I got unlucky and picked a variation that did poorly during this timeframe but many of my other choices did well. My strategy concept held up but just not the one I picked. That is wrong because what we want to know is did our strategy concept hold up in OOS.
Imagine the reverse scenario. Your strategy concept sucks and it behaves as well as choosing random entry and exit times. In this case, you could get “lucky” and pick a variation that does well in OOS data. Now you are off trading a strategy that is as good as random.
Final Thoughts
In the next post, I will show results of doing an IS and OOS testing on a mean reversion strategy and how picking only one variation can be dangerous. Then I will show how using a set of variations is a much better way to help determine if your strategy did well in OOS testing. The post will also show how one can come to different conclusions depending on how the IS and OOS ranges are chosen.
While waiting for the next post, you can read Optimization Mean Reversion which covers some of what I will next.
Good Quant Trading,