- in General , Research by Cesar Alvarez
Benford’s Law and Strategy Selection
While talking to a trader, he mentioned an article in the December 2021 issue of Technical Analysis of Stocks & Commodities about Benford’s Law. I had read the same article and was wondering how it could be applied to my trading. Benford’s Law is often used to look for fraud. I am sure I am not committing fraud on myself. As we talked, we wondered whether this could help in selecting which strategy to trade from an optimization?
Benford’s Law Summary
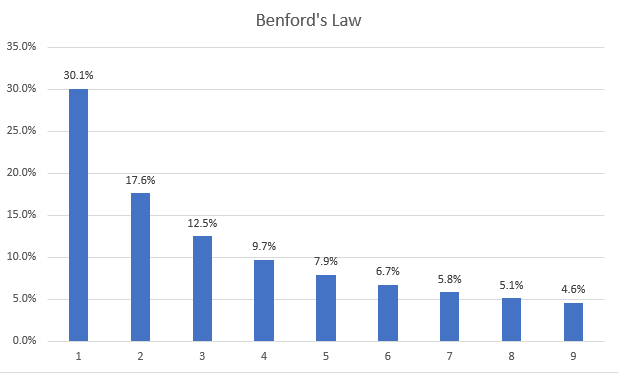
According to Benford’s Law, in a large set of numbers the significant digit is not evenly distributed but the digit “1” occurs the most frequently and the digit “9” the least. The theoretical distribution is shown in this chart.
In general, for a data set to follow Benford’s Law, the data set should have the following properties
- Several orders of magnitude between the smallest and largest values
- Either the minimum or maximum should be unbounded
- Data set with more than a couple thousand numbers
- The data is not concentrated around the mean
For more information about Benford’s Law, these are two good articles. What is Benford’s Law and why is it important for data science? and Wikipedia’s article Benford’s law.
Application to stock data
Using the percentage daily return on stock data, here is how the data properties fit with what Benford’s Law wants in a data set
- Yes, the data have several orders of magnitude
- Maximum is unbounded
- 10 years of a single stock is 2500 data points. More would be better.
- Returns are concentrated around the mean. This is not what we want.
The data are not a perfect fit, but we will try and see what we get.
SPY
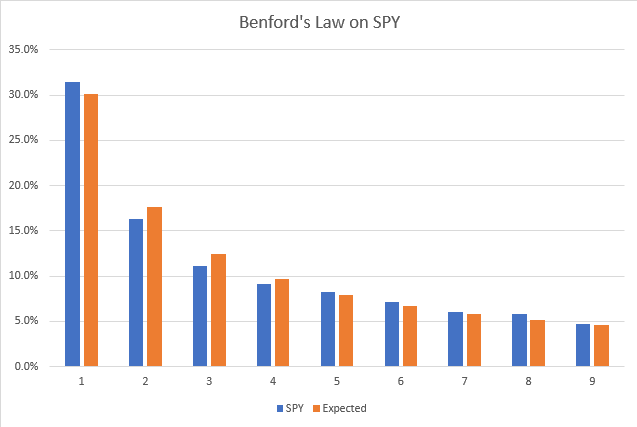
From 2007 to 2021, here are the results of the significant digit count on the daily percentage return on the SPY
Visually the SPY appears to follow Benford’s Law. There are several statistical methods for determining if it does follow. I will be using the Chi-Square Statistic. What we need to know about this value is the lower the better. If there was a perfect match between the data set and the theoretical distribution, the value would be zero. Typically, a value under 15.5 is used to determine if the data does follow Benford’s Law. The Chi-Square Statistic for the SPY data is 17.9. Close to the cutoff. I guess perhaps the SPY is slightly manipulated.
S&P500 Stocks
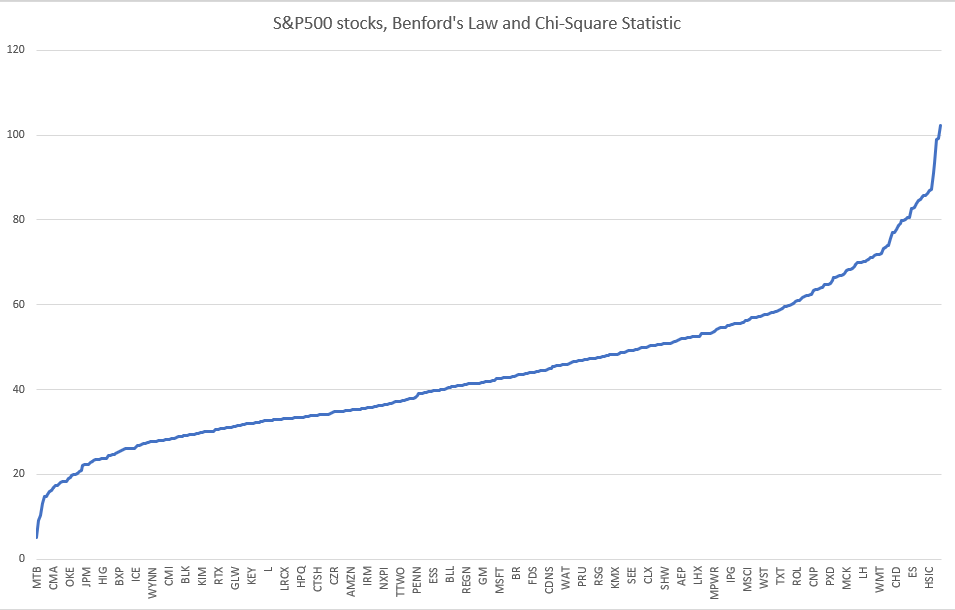
Next, I was curious about how the individual stocks of the S&P500 behaved. I used the current S&P 500 stocks and data from 2007 to 2021.
Values for the Chi-Square range from a low of 5 for MTB to a high of 102 for AWK. The average for all was 44.4. Only seven stocks had values under 15.5. Either one of two things is going on here. One, these stocks are highly manipulated. Or two, the data is not a good fit to apply Benford’s Law. I am going with number two because I am an optimist and believe the markets are only slightly manipulated.
Momentum Strategy
Now to what I wanted to know. Is there any predictive value here for selecting a strategy from an optimization run?
I ran an optimization (432 runs) on a momentum strategy that I trade from 2007 to 2016. I took the top 1/3 of the runs (145 runs) based on CAR and computed the Chi-Square Statistic for each based on the daily % return of the strategy. From the Chi-Square Statistic, I divided these into terciles.
Side note: I thought the Chi-Square Statistic was big for the S&P 500 stocks. In my optimization run, the range was from 210 to 2143. Not even close to following Benford’s Law!
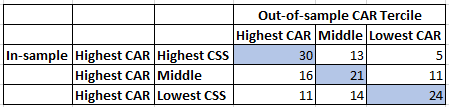
Then using an out-of-sample optimization, I computed the CAR tercile that each of these in-sample runs fell into. My hypothesis was that failure to follow Benford’s Law implied a higher potential for curve fitting, which then implies that those in-sample runs in the top tercile for CAR and bottom tercile for Chi-Square Statistic would again end up in the top tercile for CAR in the out-of-sample.
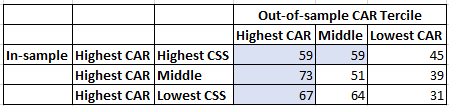
The numbers in the table represent how many runs fell into that cell, with a blue background highlighting the highest value in that row The first row represents 48 runs from the in-sample that fell into the top tercile by CAR and then the top tercile by Chi-Square Statistic for that top tercile. The blue 30 then means that 30 of those 48 runs end up in the top tercile by CAR in the out-of-sample.
At first, I was excited by the very clear diagonal line and the fact that the other cells followed what I expected. But then I realized this was the opposite of what I thought. I expected the lowest tercile by Chi-Square Statistic to be most likely to stay in the top CAR tercile. I started making up stories to explain this, but then I realized I should test this on a different strategy.
Mean Reversion Strategy
Following the same process that I used for the momentum strategy, here are the results of a mean reversion strategy.
Now, it is random. No pattern at all. Too bad.
Thanks
I want to thank Matt Radtke for helping proof this article. The first time I sent it to him, he caught a huge logical mistake that I had made. It would have been embarrassing to publish an article with such a bad mistake. That is also the reason it has been so long since my last post. I had to redo a lot of the work I had done.
Final Thoughts
As often happens in research, an interesting idea leads nowhere. Given that the data do not follow the requirements for applying Benford’s Law, I am not too surprised by the results. This was a good lesson for me on not stopping when I got the first good results. Even had the results panned out, I am not sure I would have used them. No story that I could make about why this should work made me comfortable. And we must be comfortable with the reasons we are trading our strategies.
Backtesting platform used: AmiBroker. Data provider: Norgate Data (referral link)
Good quant trading,